We awe at Donald Knuth. I wondered, if I can understand a subject taught by Knuth and derive satisfaction of learning
something directly from the master. I attended his most recent lecture on "comma free codes", felt that it was
accessible and could be understood by putting some effort. This is my attempt to grasp the topic of "comma free codes",
taught by Knuth for his 21st annual christmas tree lecture on Dec 2015. We will use some definitions directly from
Williard Eastman's paper, reference the topics in wikipedia, look at Knuth's explanation.
We talk of codes in the context of information theory. A code is a system of rules to convert information—such as a
letter, word, sound, image, or gesture—into another form or representation. A sequence of symbols, like a sequence of
binary symbols, sequence of base-10 decimals or a sequence of English language alphabets can all be termed as "code". A
block code is a set of codes having the same length.
Comma Free Block Code
Comma free code is a code that can be easily synchronized without any external unit like comma or space,
"likethis". Comma free block code is set of same length codes having the comma free property.
The four letter words in "goodgame" is recognizable, it easy to derive those as "good" and "game".
Other possible substring four letter words in that phrase "oodg", "odga", "dgga" are invalid words in
english (or non code-words) and thus we did not have any problem separating the codewords when they were not
separated by delimiters like space or comma. Anecdotally, Chinese and Thai languages do not use space between words.
Take an alternate example, "fujiverb". Can you say deterministically if the word "jive" is my code word? Or my
code words consists only of "fuji" and "verb". You cannot determine it from this message and thus, "fuji" and
"verb" do not form valid a "comma free block codes".
The same applies to a periodic code word like "gaga". If a message "gagagaga" occurs, then the middle word
"gaga" will be ambiguous as it is composed of 2-letter suffix and a 2-prefix of our code word and we wont be able to
differentiate it.
Mathematical definition
Comma free code words are defined like this.
A block code, C containing words of length n is called comma free if, and only if, for any words
\(w = w_1, w_2 ... w_n. \: and \: x = x_1, x_2 ... x_n\) belonging to C, the n letter overlaps
\(w_k ... w_nx_1 .... x_{k-1} (k = 2, ... n)\) are not words in the code.
This simply means that if two code words are joined together, than in that joined word, any substring from second letter
to the last of the block code length should not be a code word.
How to find them?
Backtracking.
The general idea to find comma free block codes is use a backtracking solution and for every word that we want to add to
the list, prune through through already added words and find if the new word can be a substring of two words joined
together from the existing list. Knuth gave a demo of finding the maximum comma free subset of the four letter words.
commafree_check.py (Source)
def check_comma_free(input_string):
if check_periodic(input_string):
print("input string is periodic, it cannot be commafree.")
return
if len(comma_free_words) == 0:
comma_free_words.append(input_string)
else:
parts = get_parts(input_string)
for head, tail in parts:
if (any_starts_with(head) and any_ends_with(tail)) or (any_starts_with(tail) and any_ends_with(head)):
print("%s|%s are part of the previous words." % (head, tail))
return
comma_free_words.append(input_string)
This logic is dependent on the order in which comma free block codes are analyzed. For finding a maximal set in a given
alphabet size in any order a proper backtracking based solution should be devised, which considers all the cases of
insertions.
How many are there?
Backtracking based solution requires us to intelligently prune the search space. Finding effective strategies for
pruning the search space becomes our the next problem in finding the comma free codes. We will have to determine how
many comma free block codes are possible for a given alphabet size and for a given length.
For 4 letter words, (n = 4) of the alphabet size m, we know that there are \(m^4\) possible words (permutation
with repetition). But we're restricted to aperiodic words of length 4, of which there are \(m^4 - m^2\). Notice
further that if word, item has been chosen, we aren't allowed to include any of its cyclic shifts temi, emit*,
or mite, because they all appear within itemitem. Hence the maximum number of codewords in our commafree code
cannot exceed \((m^4 - m^2)/4\).
Let us consider the binary case, m = 2 and length n = 4, C(2, 4). We can choose four-bit "words" like this.
[0001] = {0001, 0010, 0100, 1000},
[0011] = {0011, 0110, 1100, 1001},
[0111] = {0111, 1100, 1101, 1011},
The maximum number of code words from our formula will be \(2^4 - 2^2/4 \: = \: 3\). Can we choose three
four-bit "words" from the above cyclic classes? Yes and choosing the lowest in each cyclic class will simply do. But
choosing the lowest will not work for all n and m.
In the class taught by Knuth, we analyzed the choosing codes when m = 3 {0, 1, 2} and for n = 3, C(3, 3). The words
in the category were
000 111 222 # Invalid since they are periodic
001 010 100 # A set of cyclic shifts, only one can taken as a valid code word.
002 020 200
011 110 101
012 120 201
021 210 102
112 121 211
220 202 022
221 212 122
The number 3-alphabet code words of length 3 is 27 ( = \(3^3\)). The set of valid code words in this will be
\((3^3-3) / 3 = 8\).
Choosing the lowest index will not work here for e.g, if we choose 021 and 220, and we send the word 220021 the word 002
is conflicting as it is part of our code word. With any back-tracking based solution, we will have to determine the
correct non-cyclic words to choose in each set to form our maximal set of 8 code words.
The problem of finding comma free code words increases exponentially to the size of the length of the code word and on
the code word size. For e.g, The task of finding all four-letter comma free codes is not difficult when m = 3, and only
18 cycle classes are involved. But it already becomes challenging when m = 4, because we must then deal with \((4^4
- 4^2) / 4 = 60\) classes. Therefore we'll want to give it some careful thought as we try to set it up for backtracking.
Willard Eastman came up with clever solution to find a code word for any odd word length n over an infinite alphabet
size. Eastman proposed a solution wherein if we give a n letter word (n should be odd), the algorithm will output the
correct shift required to make the n letter word a code word.
Eastman's Algorithm
Construction of Comma Free Codes
The following elegant construction yields a comma free code of maximum size for any odd block length n, over any
alphabet.
Given a sequence of \(x =x_0x_1...x_{n-1}\) of nonnegative integers, where x differs from each of its
other cyclic shifts \(x_k...x_{n-1}x_0..x_{k-1}\) for 0 < k < n, the procedure outputs a cyclic shift
\(\sigma x\) with the property that the set of all such \(\sigma x\) is a commafree.
We regard x as an infinite periodic sequence \(<x_n>\) with \(x_k = x_{k-n}\) for all \(k \ge n\). Each
cyclic shift then has the form \(x_kx_{k+1}...x_{k+n-1}\). The simplest nontrivial example occurs when n = 3,
where \(x=x_0 x_1 x_2 x_0 x_1 x_2 x_0 ...\) and we don't have \(x_0 = x_1 = x_2\). In this case, the algorithm
outputs \(x_kx_{k+1}x_{k+2}\) where \(x_k > x_{k+1} \le x_{k+2}\); and the set of all such triples clearly
satisfies the commafree condition.
The idea expressed is to choose a triplet (a, b, c) of the form.
\begin{equation*}
a \: \gt b \: \le c
\end{equation*}
Why does this work?
If we take two words, xyz and abc following this property, combining them we have,
\begin{equation*}
x \: \gt y \: \le z \quad a \: \gt b \: \le c
\end{equation*}
There by none of the substrings will be a code word and we can satisfy the comma free property.
And if we use this condition to determine the code words in our C(3,3) set, we will come up with the following
codes which can form valid code words.
000 111 222
001 010
100
002 020
200
011 110
101
012 120
201
021 210
102
112 121
211
220
202 022
221
212 122
The highlighted words will form valid code words and all of these satisfy the criteria, \(a \: \gt b \: \le c\)
Now, if you are given a word like 211201212, you know for sure that they are composed of 211, 201 and
212 as none of other intermediaries like (112, 120, 201, 012, 121) occur in our set.
Eastman's algorithm helps in finding the correct shift required to make any word a code word.
For e.g,
Input: 001
Output: Shift by 2, thus producing 100
Input: 221
Output: Shift by 1, thus producing 212
And the beauty is, it is not just for words of length 3, but for any odd word length n.
The key idea is to think of x as partitioned into t substrings by boundary marked by \(b_j\) where
\(0 \le b_0 \lt b_1 \lt ... \lt b_{t-1} < n\) and \(b_j = b_{j-t} + n\) for \(j \ge t\). Then substring
\(y_j\) is \(x_{b_j} x_{b_{j+1}-1}\). The number t of substrings is always odd. Initially, t = n and
\(b_j = j\) for all j; ultimately t = 1 and \(\sigma x = y0\) is the desired output.
Eastman's algorithm is based on comparison of adjacent substrings \(y_{j-1} and y_j\). If those substring have
the same length, we use lexicographic comparison; otherwise we declare that the longer string is bigger.
The number of t substring is always odd because we went with an odd string length (n).
The comparison of adjacent substring form the recursive nature of the algorithm, we start with small substring of
length 1 adjacent to each other and then we find compare higher length substring, whose markers have been found by
the previous step. This will become clear as we look the hand demo.

Basin and Ranges
It's convenient to describe the algorithm using the terminology based on the topograph of Nevada. Say that i is a
basin if the substrings satisfy \(y_{i-1} \gt y_i \le y_{i+1}\). There must be at least one basin; otherwise all
the \(y_i\) would be equal, and x would equal one of its cyclic shifts. We look at consecutive basins, i and j;
this means that i < j and that i and j are basins, and that i+1 through j - 1 are not basins. If there's only one
basin we have \(j = i + t\). The indices between consecutive basins are called ranges.
The basin and ranges is Knuth's terminology, taken from the book Basin and Ranges by John McPhee which describes the
topology of Nevada. It is easier to imagine the construct we are looking for if we start to think in terms of basin and
ranges.
Since t is odd, there is an odd number of consecutive basins for which \(j - i\) is odd. Each round of Eastman's
algorithm retains exactly one boundary point in the range between such basins and deletes all the others. The
retained point is the smallest \(k = i + 2l\) such that \(y_k \gt y_{k+1}\). At the end of a round, we reset
t to the number of retained boundary points, and we begin another round if t > 1.
Word of length 19
Let's work through the algorithm by hand when n = 19 and x = 3141592653589793238
Phase 1
3 | 1 | 4 | 1 | 5 | 9 | 2 | 6 | 5 | 3 | 5 | 8 | 9 | 7 | 9 | 3 | 2 | 3 | 8 . 3 | 1 | 4 | 1 | 5
Next we go about identifying basins. We identify the basins where for any 3 numbers (a, b, c), \(a \: \gt b
\le c\) and put the markers below them
After the cyclic repetition we see the repetition of the basin. Like the last line below 1 is same as the first
line. It is the basin that is repeated.
3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 3 1 4 1 5
| | | | | | . |
3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 3 1 4 1 5
---|--e--|---o----|---o----|-----e-----|---o----|-----e--.--|--------
Next, take all the odd length basin markers, go by steps of 2, 4, 6 so on and identify the first greater than
number and place the new basin markers before them.
For e.g, in 1-5-9-2. The 2 length path is "1-5-9" and first higher will be 9 and we have to place the marker ahead of
it. So, the phase 0 of eastman algorithm will output, 5, 8 and 15. denoting the indices where our basins are after the
first phase.
If you are watching the video with Knuth giving a demo, there is a mistake in the video that second basin identifier
is placed after 5, instead of before 5 (We should go by steps of 2 and place it before the first greater than number).
3 1 4 1 5 | 9 2 6 | 5 3 5 8 9 7 9 | 3 2 3 8 . 3 1 4 1 5
Phase 2
In the second phase, we use the basin markers of the previous phase and compare the sub strings denoted by the basin.
We take the substring of length 19, but now denoted by basins. The repetition of the string in the previous steps
helped us here.
9 2 6 | 5 3 5 8 9 7 9 | 3 2 3 8 3 1 4 1 5
9 2 6 5 3 5 8 9 7 9 | 3 2 3 8 3 1 4 1 5
At the end of Phase 2, the algorithm outputs index 15, as the shift required to create the code word out of 19 word
string. And thus our code word found by the eastman's algorithm is
3 2 3 8 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9
Knuth's gave a demo with his implementation in CWEB. He shared a thought that even though algorithm is expressed
recursively, the iterative implementation was straight forward. For the rest of the lecture he explores the
algorithm on a binary string of PI of n = 19 and finds the shift required. Also, gives the probability of Eastman's
algorithm finishing in one round, that is, just the phase 1.
All these are covered as exercises and answers in the pre-fascicle 5B of his volume 5 of The Art of Computer
Programming, which can be explored in further depth.
Video
References
Tidbits
The Emerald Route is a travelogue by R. K. Narayan. It was published by Indian Thought Publications in 1980. It is a pseudo-travel guide for Karnataka, India. The book was commissioned by the Government of Karnataka, and the initial non-commercial version was published in 1977 as part of a government publication. The book is focused on local history, culture and heritage, and does not exhibit much of Narayan's characteristic personal narrative.
is a travelogue written by R.K. Narayan. In this book, he
details the cultural and mythological history of various cities in Karnataka.
Narayan presents the mythological history alongside factual accounts of the
places, offering readers a glimpse into his unique perspective. He narrates
these stories as if they are true events that occurred in those locations.
Adi Shankara (8th c. CE), also called Adi Shankaracharya (Sanskrit: आदि शङ्कर, आदि शङ्कराचार्य, romanized: Ādi Śaṅkara, Ādi Śaṅkarācārya, lit. 'First Shankaracharya', pronounced [aːd̪i ɕɐŋkɐraːt͡ɕaːrjɐ]), was an Indian Vedic scholar-monk and teacher (acharya) of Advaita Vedanta, who has popular become known as a major religious hero due to 14th century political and religious developments. While he is often revered as the most important Hindu philosopher, reliable information on Shankara's actual life is scant, and the historical influence of his works on Hindu intellectual thought has been questioned. The historical Shankara was probably relatively unknown and Vaishna-oriented. His true impact lies in his "iconic representation of Hindu religion and culture," despite the fact that most Hindus do not adhere to Advaita Vedanta.
, who was born with a
predetermined lifespan of 16 years. Determined to make the most of his time,
Sankara studied all the scholarly works by the age of 10, became a monk, and
began preaching. When he turned 16, a debate took place between
Vyasa
Vyasa (; Sanskrit: व्यास, lit. 'compiler, arranger', IAST: Vyāsa) is a rishi (sage) with a prominent role in most Hindu traditions. He is also known as Veda Vyasa (Sanskrit: वेदव्यास, lit. 'the one who classified the Vedas', IAST: Vedavyāsa) or Krishna Dvaipayana (Sanskrit: कृष्णद्वैपायन, IAST: Kṛṣṇadvaipāyana). Traditionally regarded as the author of the epic Mahābhārata, Vyasa also plays a prominent role as a character. He is also regarded by the Hindu traditions to be the compiler of the mantras of the Vedas into four texts, as well as the author of the eighteen Purāṇas and the Brahma Sutras.
and
Sankara. Vyasa, the original author of the work Sankara was discussing, engaged
in a prolonged debate with him. Unaware of Vyasa's identity, Sankara held firmly
to his stance. When the debate showed no signs of resolution, one of Sankara's
students called for a truce. Impressed by Sankara's profound knowledge of his
own work, Vyasa granted him a boon to live for another 16 years.
Srirangapatna or Srirangapattana is a town and headquarters of one of the seven Taluks of Mandya district, in the Indian State of Karnataka. It gets its name from the Ranganathaswamy temple consecrated around 984 CE. Later, under the British rule, the city was renamed to Seringapatam. Located near the city of Mandya, it is of religious, cultural and historic importance.
, where, during one of the
battles that
Tipu_Sultan
Tipu Sultan (Urdu: [ʈiːpuː sʊlt̪aːn], Kannada: [ʈipːu sult̪aːn], Sultan Fateh Ali Sahab Tipu; 1 December 1751 – 4 May 1799), commonly referred to as Sher-e-Mysore (Tiger of Mysore), was the Sultan of Mysore from 1782 until his death in 1799. He was a pioneer of rocket artillery. He expanded the iron-cased Mysorean rockets and commissioned the military manual Fathul Mujahidin. The economy of Mysore reached a zenith during his reign. He deployed rockets against advances of British forces and their allies during the Anglo-Mysore Wars, including the Battle of Pollilur and Siege of Srirangapatna.
lost, he was forced to surrender two of his sons,
aged 9 and 11, as hostages to the British as part of the conditions of
surrender. It is said that Tipu Sultan later managed to secure their release by
paying a substantial ransom to the British.


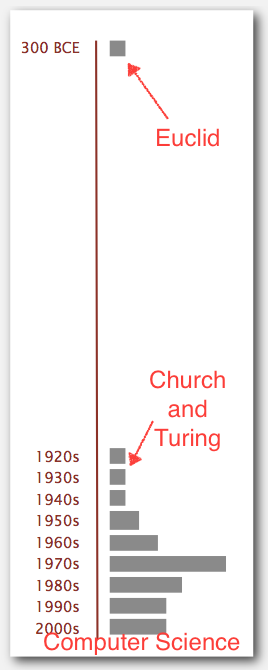 Algorithms have started making difference in our lifes since 1970s and are in their prime now.
Algorithms have started making difference in our lifes since 1970s and are in their prime now.




