What is the proof that total number of subsets of a set is 2^n?

I have known "by heart" that total number of the subsets of a set of n number is \(2^n\) I was struggling to find an intuitive explanation, and two answers helped me to understand it.

For each element, you have two choices: either you put it in your subset, or you don't; and these choices are all independent.

Citation:

Bruno Joyal (https://math.stackexchange.com/users/12507/bruno-joyal), What is the proof that the total number of subsets of a set is $2^n$?, URL (version: 2013-10-31): https://math.stackexchange.com/q/546417

Another was this table that represented the sets as binary, to denote 0 as an absence of the element and 1 as presence of the element.

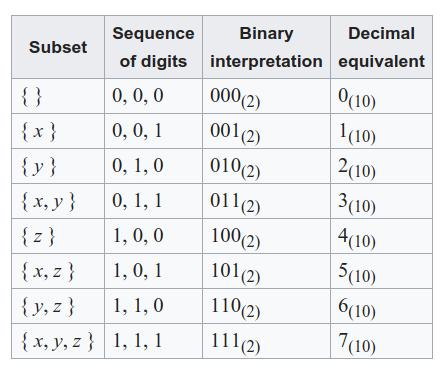
That can help us understand that the total number of subsets of set of n is \(2^n\)